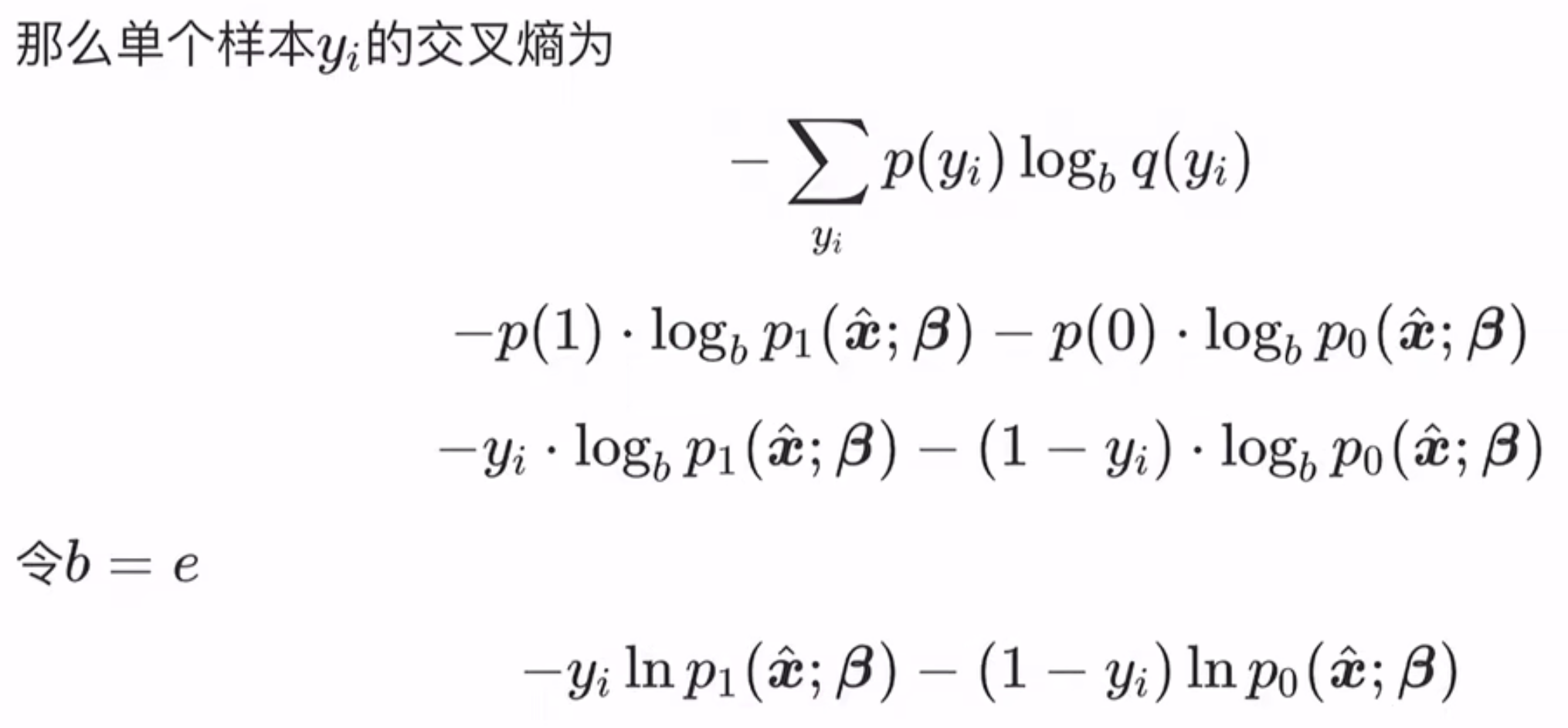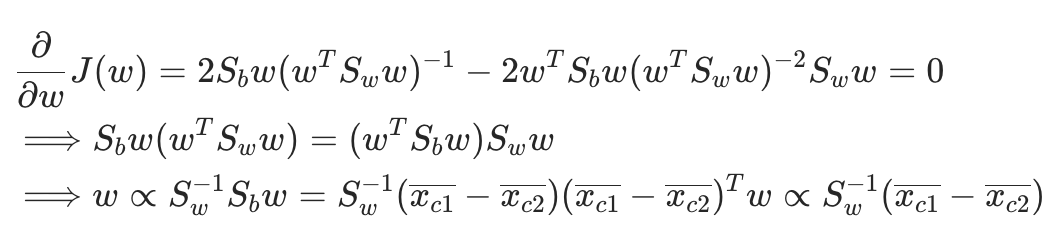线性回归 主要 follw 教程:https://datawhale.feishu.cn/docs/doccndJC2sbSfdziNcahCYCx70W#
机器学习三要素
模型:根据具体问题,确定假设空间
策略:根据评价标准,确定选取最优模型的策略(通常会产出一个“损失函数”)
算法:求解损失函数,确定最优模型
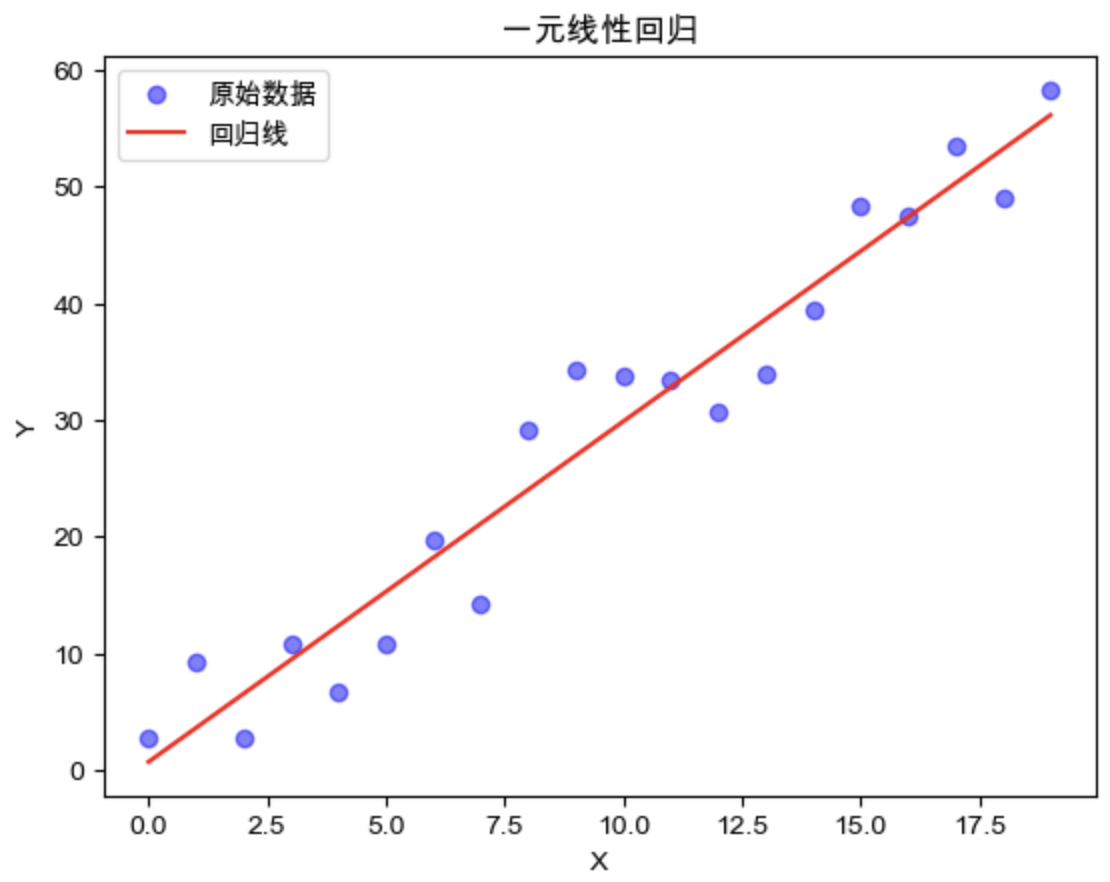
一元线性回归 以一元线性回归为例:求解发际线高度x和计算机水平y的关系。
模型:根据经验(或观察数据形态),呈线性关系,所以假设空间 $f(x)=wx+b$,而不是曲线关系。
策略:所有点距离拟合的直线垂直距离最小,即均方误差小,最小二乘法。或者使用极大似然估计,假设$y=wx+b+\epsilon$,对$\epsilon$误差建模,能得出同样策略。
算法:可以证明 $E_{(w, b)}$是凸函数(可以求2阶偏导数,证明Hessian矩阵半正定),所以能求出闭式解。(但机器学习算法通常没有闭式解,就要用梯度下降法、牛顿法近似求解)
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import numpy as npimport matplotlib.pyplot as pltdef load_data (n, w_true, b_true ): X = np.arange(n) eps = -0.5 * b_true + np.random.random(n) * b_true Y = w_true * X + eps return X, Y def closed_form_solution (X,Y ): X_bar = X.sum () / X.size Y_bar = Y.sum () / Y.size w = Y.dot(X - X_bar) / (X.dot(X) - (X.sum ()) ** 2 / X.size) b = Y_bar - w * X_bar return w, b X, Y = load_data(20 , 3 , 15 ) w, b = closed_form_solution(X, Y) Y_predict = X * w + b plt.scatter(X, Y, label="原始数据" , c='b' , alpha=0.5 ) plt.plot(X, Y_predict, label="回归线" , c='r' ) plt.title('一元线性回归' ) plt.xlabel("X" ) plt.ylabel("Y" ) plt.legend() plt.show()
结果可视化:
1 2 3 4 5 6 7 8 plt.scatter(X, Y, label="原始数据" , c='b' , alpha=0.5 ) plt.plot(X, Y_predict, label="回归线" , c='r' ) plt.title('一元线性回归' ) plt.xlabel("X" ) plt.ylabel("Y" ) plt.legend() plt.show()
多元线性回归 与一元线性回归相比,$\boldsymbol{x}$维度变高,写成向量形式:
把$\boldsymbol{w}$和$b$合并成$\boldsymbol{\hat w}$:
故多元线性回归的均方误差可以写成:
其中:
所以可以把$E_{\hat{\boldsymbol{w}}}$向量化为:$E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})$
同样可以证明$E_{\hat{\boldsymbol{w}}}$是凸函数(求二阶偏导证明hessian矩阵半正定),$E_{\hat{\boldsymbol{w}}}$对$\hat{\boldsymbol{w}}$求一阶偏导:
其中用到的矩阵微分公式:$\frac{\partial \boldsymbol{x}^{\mathrm{T}} \boldsymbol{a}}{\partial \boldsymbol{x}}=\frac{\partial \boldsymbol{a}^{\mathrm{T}} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{a}, \frac{\partial \boldsymbol{x}^{\mathrm{T}} \mathbf{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\left(\mathbf{A}+\mathbf{A}^{\mathrm{T}}\right) \boldsymbol{x},\frac{\partial \mathbf{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\mathbf{A}^{\mathrm{T}}$
再令一阶偏导为零,可以求得闭式解:
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 import numpy as npimport matplotlib.pyplot as pltdef load_data (n_sample:int , W_true:np.array, b_true ): n_feature = len (W_true) ones = np.ones(shape=(n_sample,1 )) X = np.concatenate([np.random.random((n_sample, n_feature)), ones],axis=1 ) eps = -0.5 * b_true + np.random.random(n_sample) * b_true W_true = np.concatenate([W_true,[1 ,]],axis=0 ) W_true = np.mat(W_true).T Y = X * W_true + np.mat(eps).T return X, Y def closed_form_solution (X, Y ): X = np.mat(X) Y = np.mat(Y) XTX = X.T * X if np.linalg.det(XTX) == 0 : print ('X^T·X 不是满秩矩阵,解不唯一' ) return W = XTX.I * X.T * Y return W def gradient_descent_trainer (X:np.matrix, Y:np.matrix, W:np.matrix, lr:float ): gradient = 2 * X.T * (X * W - Y) W = W - lr * gradient return W def loss_function (X:np.matrix, Y:np.matrix, W:np.matrix ): return float ((Y - X * W).T * (Y - X * W)) def gradient_descent_solution (X, Y, epoch, lr ): X = np.mat(X) Y = np.mat(Y) W = np.mat(np.random.random((X.shape[1 ],1 ))) lossList = [] for i in range (epoch): loss = loss_function(X, Y, W) lossList.append(loss) if (i+1 )%10 ==0 : print (f"epoch:{i+1 } loss:{loss:.4 f} " ) W = gradient_descent_trainer(X, Y, W, lr) return W, lossList
1 2 3 4 5 6 7 8 9 10 11 12 13 14 n_sample = 10 W_true = np.array([1 ,2 ,3 ,4 ,5 ]) b_true = 1 X,Y = load_data(n_sample, W_true, b_true) W_1 = closed_form_solution(X, Y) Y_1 = X * W_1 epoch = 200 lr = 1e-2 W_2, lossList = gradient_descent_solution(X, Y, epoch, lr) Y_2 = X * W_2
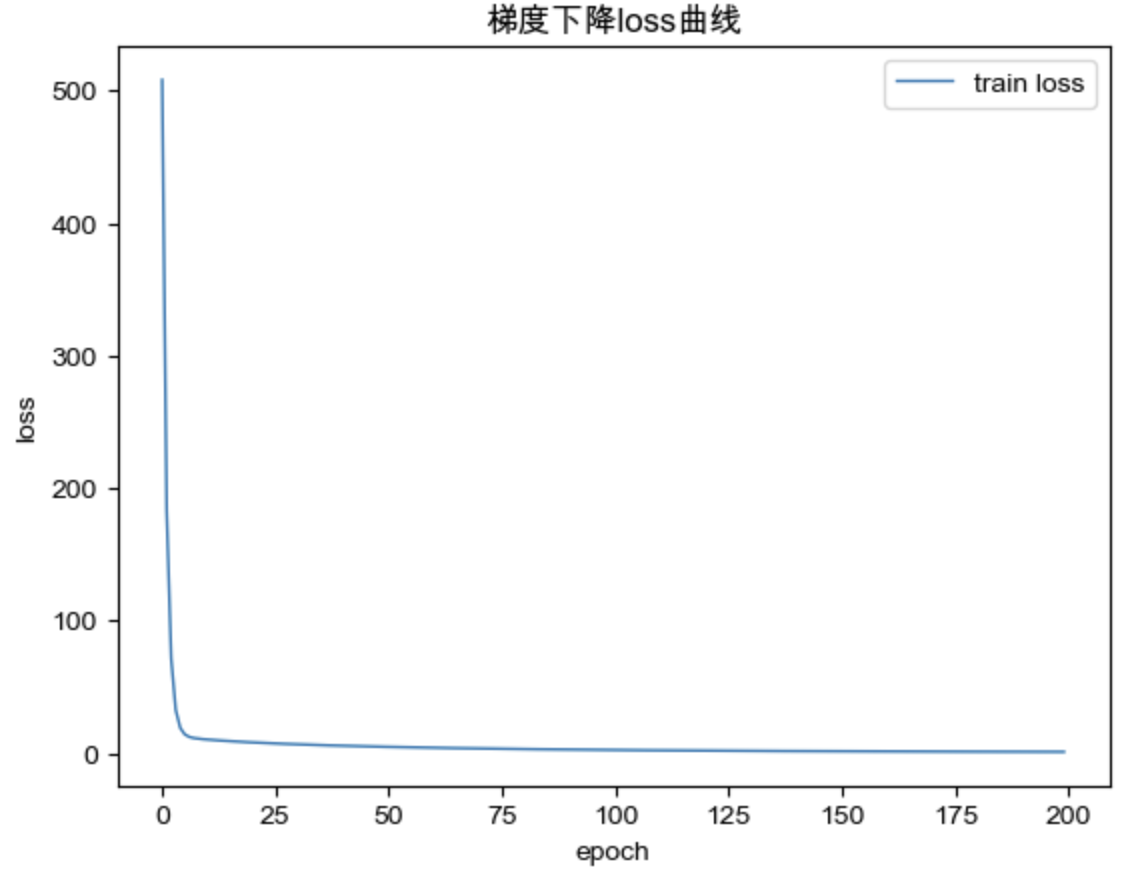
梯度下降 loss 曲线:
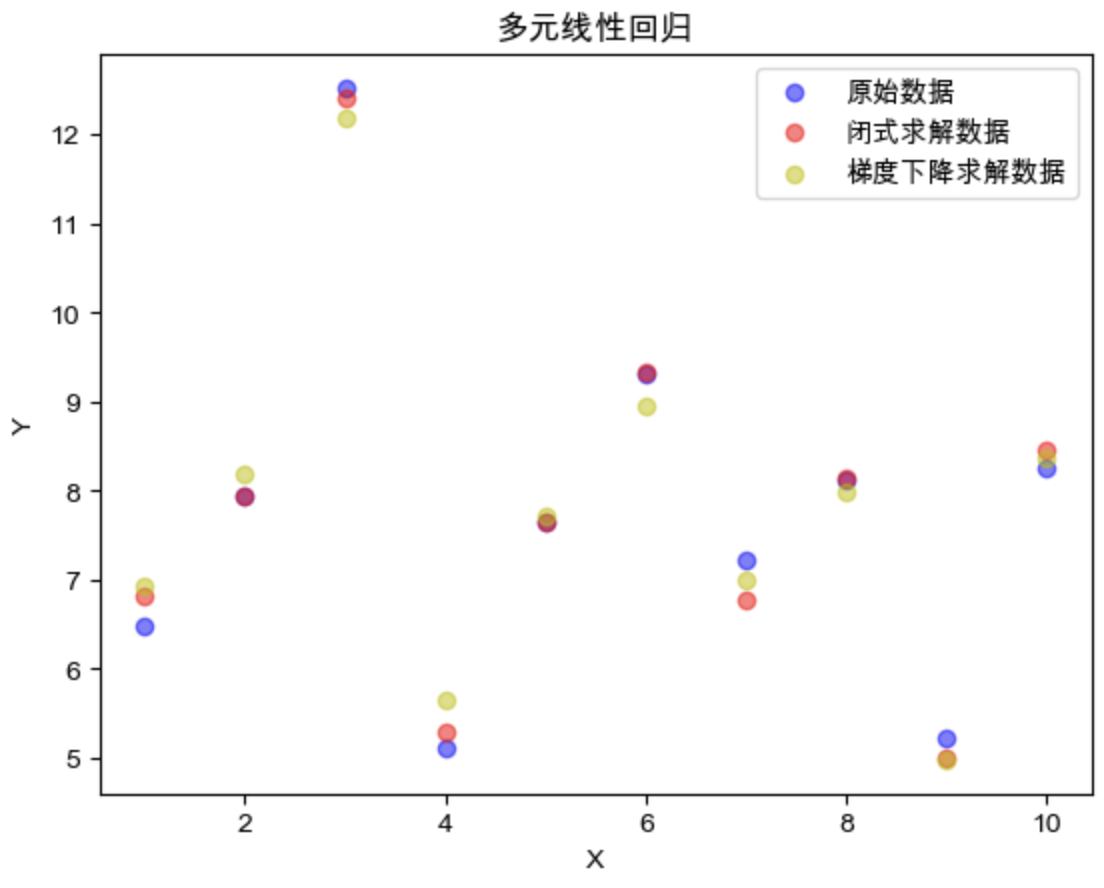
结果可视化:
1 2 3 4 5 6 7 8 9 plt.scatter(list (range (1 ,n_sample+1 )), Y.tolist(), label="原始数据" , c='b' , alpha=0.5 ) plt.scatter(list (range (1 ,n_sample+1 )), Y_1.tolist(), label="闭式求解数据" , c='r' , alpha=0.5 ) plt.scatter(list (range (1 ,n_sample+1 )), Y_2.tolist(), label="梯度下降求解数据" , c='y' , alpha=0.5 ) plt.title('多元线性回归' ) plt.xlabel("X" ) plt.ylabel("Y" ) plt.legend() plt.show()
对数几率回归(逻辑回归 LR) 对数几率回归算法的机器学习三要素:
模型:线性模型,输出值的范围是(0,1),近似阶跃的单调可微函数
策略:极大似然估计,信息论,殊途同归
算法:梯度下降,牛顿法
对数几率回归(逻辑回归):用线性模型做二分类任务
用sigmoid函数,将实数域的取值映射到(0,1):
为什么可以用sigmoid? 西瓜书上的解释:$y =\frac{1}{1+e^{- \left( \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b \right)}}$ 可以推导出 $\frac{y}{1-y}= \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$,若将$y$视作样本$\boldsymbol{x}$作为正例的可能性, 则$1-y$是样本$\boldsymbol{x}$作为负例的可能性,$\frac{y}{1-y}$反应了样本$\boldsymbol{x}$作为正例的相对可能性。
损失函数推导
如果随机变量X只取0和1两个值,并且相应的概率为:
则称随机变量X服从参数为p的伯努利分布
逻辑回归是假设数据服从伯努利分布 。
在伯努利分布下,假设样本概率为:$f(n)=\left\{\begin{array}{ll}
优化均方误差? $E_{\hat{\boldsymbol{w}}}=\left(\frac{1}{1+e^{- \left( \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b \right)}}-y\right)^2$,可以证明是非凸 的,无法求解
极大似然估计法 所以考虑用极大似然估计求分布:
两边取对数:
其中:
带入$ln(L)$,可得:
因为最大化似然函数就等于最小化:
而$\mathcal{l}\left( \boldsymbol{\beta} \right)$是高阶非凸函数,所以可以用经典的数值优化方法梯度下降法或牛顿法求近似解。$\mathcal{l}\left( \boldsymbol{\beta} \right)$也是模型的损失函数。
为什么不求闭式解? 即然$\mathcal{l}\left( \boldsymbol{\beta} \right)$是高阶非凸的,可以直接解,那为什么不直接按公式求闭式解?
回忆多元线性回归的闭式解:$\hat{\boldsymbol{w}}=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y}$,这里需要求矩阵的逆,通常情况下都不存在,无法直接求解,甚至要用梯度下降近似求解的方法去求这个逆(回忆矩阵课上学的···),所以不如直接近似求解 $\hat{\boldsymbol{w}}$ 。
最大熵法 前置知识:
自信息 $I(X)=-\log _{b} p(x)$
信息熵 $H(X)=E[I(X)]=-\sum_{x} p(x) \log _{b} p(x)$,是自信息的期望,度量随机变量 $X$ 的不确定性,信息熵越大越不确定
相对熵(KL散度):度量两个分布的差异,典型使用场景是用来度量理想分布$p(x)$和模拟分布$q(x)$ 之间的差异
从机器学习三要素中“策略”的角度来说,与理想分布最接近的模拟分布即为最优分布,因此可以通过最小化相对熵 这个策略来求出最优分布。由于理想分布$p(x)$是未知但固定的分布(频率学派的角度),所以KL散度前半部分是常量,那么最小化相对熵就等价于最小化交叉熵。
这边已经等价于用极大似然估计取对数的结果了,后面依然能推导得到公式3.27
代码实现 在 MNIST 数据集上实现逻辑回归二分类,标签0~4分类为0,标签5~9分类为1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 import numpy as npimport matplotlib.pyplot as pltfrom sklearn.metrics import classification_reportdef load_mnist (fileName ): ''' 加载Mnist数据集 :param fileName:要加载的数据集路径 :return: list形式的数据集及标记 ''' print ('start to read data' ) dataArr = []; labelArr = [] fr = open (fileName, 'r' ) for line in fr.readlines(): curLine = line.strip().split(',' ) if int (curLine[0 ]) >= 5 : labelArr.append(1 ) else : labelArr.append(0 ) dataArr.append([int (num)/255 for num in curLine[1 :]]) return dataArr, labelArr def loss_fn (X:np.matrix, W:np.matrix, y:np.matrix ): y = float (y) eps = 1e-10 y_hat = float (X * W) return np.log(( 1 + np.exp(y_hat))/np.exp(y * y_hat) + eps) def lr_forward (x:np.matrix, w:np.matrix ) -> float : z = x * w return 1 /(1 + np.exp(-z)) def gradient_descent_trainer (x:np.matrix, w:np.matrix, y:np.matrix, lr:float ) -> np.matrix: y = float (y) z = x * w gradient = float ((-y + np.exp(z)/(1 +np.exp(z)))) * x.T w = w - lr * gradient return w def collate_fn (X:list , Y:list ): X = np.mat(X) Y = np.mat(Y).T ones = np.ones(shape=(X.shape[0 ],1 )) X = np.concatenate([X, ones],axis=1 ) return X, Y def evaluate (X:np.matrix, w:np.matrix, Y:np.matrix ): n_test = X.shape[0 ] y_predList = [] for idx in range (n_test): y_pred = lr_forward(X[idx],w) y_predList.append( 1 if y_pred > 0.5 else 0 ) y_truth = Y.T.tolist()[0 ] report = classification_report(y_true=y_truth, y_pred=y_predList, output_dict=True ) return report['accuracy' ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 trainData, trainLabel = load_mnist('Mnist/mnist_train.csv' ) X_train, Y_train = collate_fn(trainData, trainLabel) testData, testLabel = load_mnist('Mnist/mnist_test.csv' ) X_test, Y_test = collate_fn(testData, testLabel) w = np.random.random((X_train.shape[1 ],1 )) n_train = X_train.shape[0 ] n_test = X_test.shape[0 ] epoch = 20 lr = 1e-4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 lossTrainList = [] lossTestList = [] accTrainList = [] accTestList = [] for i in range (epoch): lossTrain4Epoch = 0 lossTest4Epoch = 0 for idx in range (n_train): y_pred = lr_forward(X_train[idx], w) w = gradient_descent_trainer(X_train[idx], w, Y_train[idx],lr) for idx in range (n_train): y_pred = lr_forward(X_train[idx], w) lossTrain = loss_fn(X_train[idx], w, Y_train[idx]) lossTrain4Epoch += lossTrain for idx in range (n_test): y_pred = lr_forward(X_test[idx], w) lossTest = loss_fn(X_test[idx], w, Y_test[idx]) lossTest4Epoch += lossTest lossTrain4Epoch /= n_train lossTest4Epoch /= n_test lossTrainList.append(lossTrain4Epoch) lossTestList.append(lossTest4Epoch) accTrain = evaluate(X_train, w, Y_train) accTest = evaluate(X_test, w, Y_test) accTrainList.append(accTrain) accTestList.append(accTest) print (f"epoch:{i+1 } " ) print (f"[Train] acc:{accTrain:.5 f} loss:{lossTrain4Epoch:.5 f} " ) print (f"[Test] acc:{accTest:.5 f} loss:{lossTest4Epoch:.5 f} " )
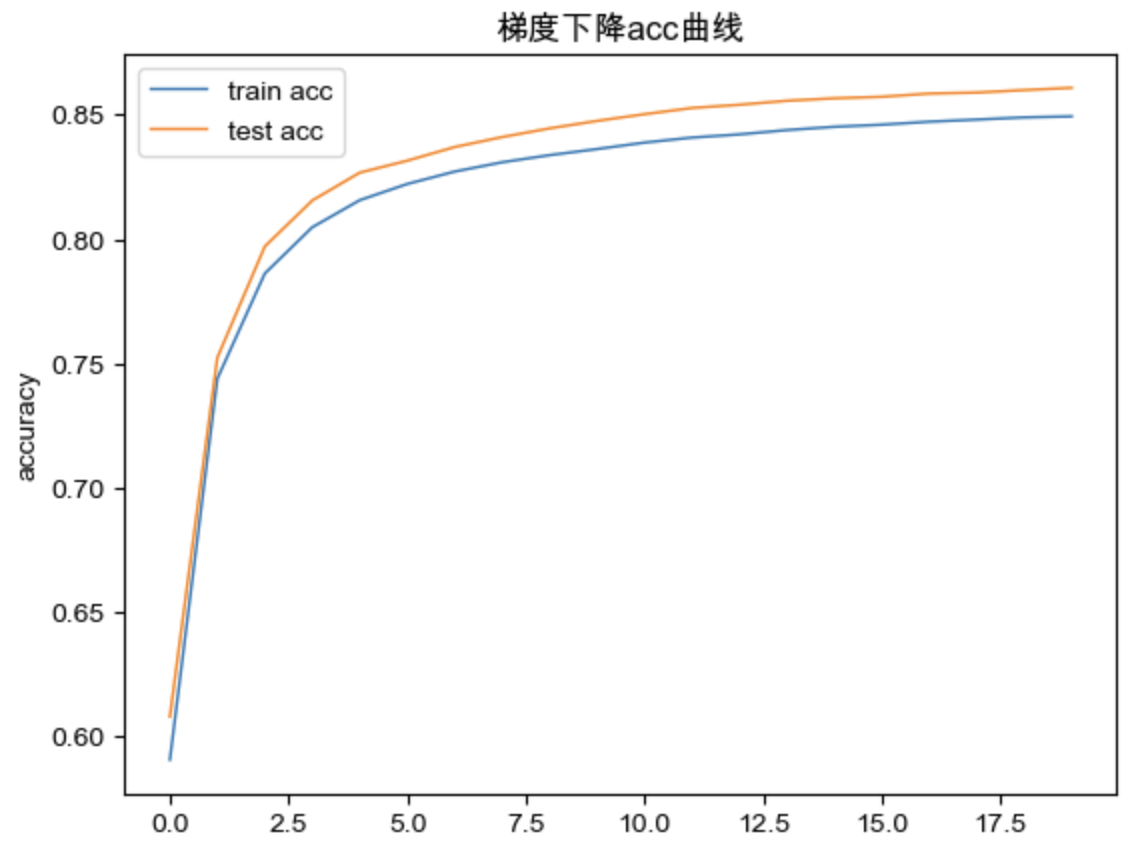
可视化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def draw_loss (lossTrain:list ,lossTest:list ): plt.plot(np.arange(len (lossTrain)), lossTrain, linewidth=1 , linestyle="solid" , label="train loss" ) plt.plot(np.arange(len (lossTest)), lossTrain, linewidth=1 , linestyle="solid" , label="test loss" ) plt.title('梯度下降loss曲线' ) plt.xlabel("epoch" ) plt.ylabel("loss" ) plt.legend() plt.show() def draw_acc (accTrain:list ,accTest:list ): plt.plot(np.arange(len (accTrain)), accTrain, linewidth=1 , linestyle="solid" , label="train acc" ) plt.plot(np.arange(len (accTest)), accTest, linewidth=1 , linestyle="solid" , label="test acc" ) plt.title('梯度下降acc曲线' ) plt.xlabel("epoch" ) plt.ylabel("accuracy" ) plt.legend() plt.show() draw_loss(lossTrainList,lossTestList) draw_acc(accTrainList,accTestList)
为什么要用sigmoid?[1]
Q:为什么 LR 模型要使用 sigmoid 函数?
A:因为bernoulli的指数族分布形式为:
其自然系数 $\eta$ 与 $\mu$ 的关系,也就是inverse parameter mapping 为 $\mu = \frac{1}{1+e^{-\eta}}$
Q:为什么要使用指数族分布?
A:因为指数族分布是给定某些统计量下熵最大的分布,例如伯努利分布就是只有两个取值且给定期望值为 $\mu$ 下的熵最大的分布。
Q:为什么要使用熵最大的分布?
A:最大熵理论
最大熵原理是在1957 年由E.T.Jaynes 提出的,其主要思想是,在只掌握关于未知分布的部分知识时,应该选取符合这些知识但熵值最大的概率分布。因为在这种情况下,符合已知知识的概率分布 可能不止一个。我们知道,熵定义的实际上是一个随机变量 的不确定性,熵最大的时候,说明随机变量最不确定,换句话说,也就是随机变量最随机,对其行为做准确预测最困难。
从这个意义上讲,那么最大熵原理的实质就是,在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断,这是我们可以作出的不偏不倚的选择,任何其它的选择都意味着我们增加了其它的约束和假设,这些约束和假设根据我们掌握的信息无法作出。
二分类线性判别分析(LDA) 算法原理 “高内聚、低耦合”的思想
从几何角度,让全体样本沿着一个方向投影(高维投影到一维),经过投影后,使得:
损失函数推导 异类样本中心尽可能远 首先是投影,我们假定原来的数据是向量$x$,那么顺着$w$方向的投影就是标量:
经过投影后,异类样本的中心尽可能远:
同类样本的方差尽可能小 我们假设属于两类的试验样本数量分别是$N_0$和$N_1$,那么我们采用方差矩阵${Var}_i$来表征每一个类内的总体分布,这里我们使用了协方差的定义:
使同类样本方差尽可能小:
综合这两点,我们用将这两个值相除来得到我们的损失函数,并最大化这个值:
注意$\mathbf{S}_{w} $和$\mathbf{S}_{b} $ 都是 $d \times d$ 的矩阵
直接对$\boldsymbol{w}$求偏导[2],因为只关心$\boldsymbol{w}$的方向:
于是求得 $\boldsymbol{w}$。
感觉这部分主要是数学,就不撸代码了。
参考 [1]https://www.zhihu.com/question/35322351
[2]https://www.bilibili.com/video/BV1aE411o7qd?p=16&vd_source=a207b39881900fb7c1580eaaa0301073